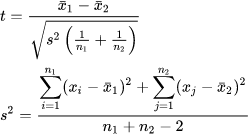آزمون تی
جهت مشاوره انجام تحلیل آماری اینجا را کلیک کنید و یا با شماره ۰۹۱۵۲۲۸۰۷۵۰ و یا ایمیل mkstatoo@gmail.com تماس بگیرید.
آزمون تی در spss
فرض صفر:
فرض صفر برای یک آزمون تی مستقل به صورت زیر می باشد
دو جامعه آماری در متغیرهای پارامتریک خود دارای میانگین های برابر هستند.
برای مثال آیا جامعه زنان و مردان هزینه برابر برای لباس خود پرداخت می کنند؟
به طور منطقی ما نمیتوانیم از کل جمعیت مردان و زنان بپرسیم که چقدر پول خرج میکنند. بنابراین ما یک نمونه از مردان و زنان را اختیار میکنیم. این نمونهها مستقل هستند زیرا با هم همپوشانی ندارند: هر کسی یا مرد است یا زن.
حالا نتایج ما از نتایج جامعه تفاوت بسیار کمی خواهد داشت. بنابراین اگر مقدار میانگین هزینه برای مردان و زنان در جامعه دقیقا برابر باشد ما هنوز مقدار تفاوت بین میانگین آنها در نمونه خواهیم دید. و نمونه ای متفاوت از یک جامعه عدد دیگری از میانگین را نشان دهد. آزمون تی به ما نشان میدهد که تفاوت بین میانگین ها به آن اندازه بزرگ هست که آن را قبول کنیم.
در مثالی دیگر محققی میخواهد بداند امتیاز روانشناسی کودکانی که والدین آنها طلاق گرفته اند متفاوت از سایر کودکان است یا خیر؟
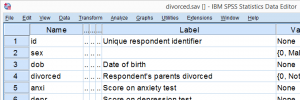
داده های جمع آوری شده در فایل divorced.sav هستند که بخشی از آنها در عکس زیر نشان داده شده است.
چهار متغیر آخر در فایل داده های ما امتیازات تست های روانشناسی مربوطه هستند. برای هر متغیر، ما از آزمون تی برای ارزیابی میانگین نمرات دو گروه کودکان استفاده خواهیم کرد.
مفروضات آزمون تی مستقل:
اگر مفروضات زیر برآورده شوند نتایج حاصل از نمونه های مستقل را می توان مورد اعتماد قرار داد:
- مشاهدات مستقل: این مورد زمانی مصداق دارد که هر رکورد که وارد نرم افزار spss می شود نشان دهنده یک فرد و یا یک واحد آماری متفاوت باشد. به نظر می رسد که این مورد برای مثال ما صادق باشد.
- نرمال بودن:متغیر وابسته باید از توزیع نرمال در جامعه پیروی کند. این فرض تنها برای نمونه های کوچک تر از حدود ۲۵ واحد مورد نیاز است.
- همگنی: انحراف استاندارد متغیر وابسته ما باید در هر دو جامعه برابر باشد. ما این فرض را تنها زمانی نیاز داریم که حجم دو نمونه ما به شدت نابرابر باشند. در صورت برقرار نبودن این فرض می توانیم از آماره تصحیح شده استفاده کنیم.
اگر این مفروضات رد شدند می توانیم از آزمون من ویتنی استفاده کنیم که معمولا آزمونی برای استفاده در متغیرهای رتبه ای می باشد.
بررسی سریع اطلاعات
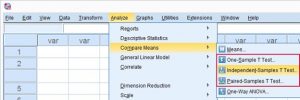
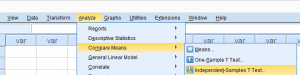
اجرای آزمون تی مستقل در نرم افزار spss
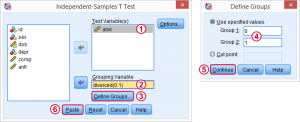
در مرحله اول یکی از چهار متغیر امتیازات را مورد آزمون قرار می دهیم. شما میتوانید طبق تصویر عمل کنید ویا با کلیک روی دکمه Paste و کپی کردن متن دستوری زیر در Syntax آزمون را اجرا کنید.
*Independent-samples t-test syntax for anxi by divorced.
(T-TEST GROUPS=divorced(0 1
MISSING=ANALYSIS/
VARIABLES=anxi/
.(CRITERIA=CI(.95/
خروجی نرمافزار SPSS برای آزمون تی نمونه مستقل
ابتدا نگاهی به آمار توصیفی گروه بندی مورد بررسی می اندازیم. اول از همه، توجه داشته باشید که تفاوت کوچکی بین میانگین نمونه ها وجود دارد. کودکانی که از فرزند طلاق هستند به طور متوسط نمره نگرانی آنها ۲۲٫۸ بوده و نمره سایر کودکان ۲۱٫۵ شده است.
خروجی آزمون تی مستقل:
 دقت داشته باشید که ما دو ردیف خروجی آزمون تی داریم. یک ردیف با فرض برابری واریانسها و یک ردیف برای نابرابری واریانسهای دو گروه مورد بررسی. خوب حالا کدام یک را باید گزارش کنیم. این که کدام ردیف نتیجه را انتخاب کنیم بستگی به نتیجه آزمون لوین برای همگنی واریانس ها دارد که قبلا در مورد اون صحبت کردیم.
دقت داشته باشید که ما دو ردیف خروجی آزمون تی داریم. یک ردیف با فرض برابری واریانسها و یک ردیف برای نابرابری واریانسهای دو گروه مورد بررسی. خوب حالا کدام یک را باید گزارش کنیم. این که کدام ردیف نتیجه را انتخاب کنیم بستگی به نتیجه آزمون لوین برای همگنی واریانس ها دارد که قبلا در مورد اون صحبت کردیم. به عنوان یک قاعده کلی اگر sig>0.05 شد ما فرض برابری واریانسها را قبول میکنیم و از ردیف اول استفاده می کنیم. در اینجا عدد مربوطه برابر sig=0.159 شده است. پس از ردیف برابری واریانسها استفاده میکنیم.
به عنوان یک قاعده کلی اگر sig>0.05 شد ما فرض برابری واریانسها را قبول میکنیم و از ردیف اول استفاده می کنیم. در اینجا عدد مربوطه برابر sig=0.159 شده است. پس از ردیف برابری واریانسها استفاده میکنیم. اگرsig(2-tailed)>0.05 شد ما معمولا فرض برابری میانگین دو جامعه را می پذیریم. sig در خروجی مقدار احتمال یا p-value گزارش می شود. تعبیری از p-value می تواند مقدار احتمال درست بودن فرض برابری میانگین دو جامعه باشد. در این مثال این مقدار برابر ۰٫۰۵۵ است. پس فرض صفر که برابری میانگین های دو گروه است را رد نمی کنیم.
اگرsig(2-tailed)>0.05 شد ما معمولا فرض برابری میانگین دو جامعه را می پذیریم. sig در خروجی مقدار احتمال یا p-value گزارش می شود. تعبیری از p-value می تواند مقدار احتمال درست بودن فرض برابری میانگین دو جامعه باشد. در این مثال این مقدار برابر ۰٫۰۵۵ است. پس فرض صفر که برابری میانگین های دو گروه است را رد نمی کنیم. df یا همان درجه آزادی که نیازی به گزارش آن در تحقیق نیست ولی معمولا آن را درج می کنیم.
df یا همان درجه آزادی که نیازی به گزارش آن در تحقیق نیست ولی معمولا آن را درج می کنیم. t که میزان آماره ما را نشان می دهد.
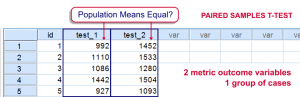
t که میزان آماره ما را نشان می دهد.آزمون تی جفتی(نمونه های جفتی) در spss
دو متغیر متریک در یک جامعه برابر هستند. هر دو متغیر برای یک عضو نمونه اندازهگیری شدهاند. اگرچه در “نمونههای جفت شده” به نظر می رسد که ما چند نمونه داریم، اما در واقع ما تنها یک نمونه و دو متغیر داریم. عکس زیر ایده اصلی این آزمون را نشان میدهد.
مثالی برای آزمون تی جفتی در spss
آزمون های t (تی)
سه نوع آزمون تی وجود دارد:
- آزمون تی تک نمونه ای
- آزمون تی مستقل
- آزمون تی جفت شده که گاهی نوع مکرر، وابسته یا همبسته نیز خوانده می شود. در این فصل هر سه آزمون t به طور مفصل توضیح داده می شود.
آزمون تی تک نمونه ای
آزمون تی تک نمونه ای که ساده ترین نوع آزمون های t است جهت تعیین این که آیا میانگین مشاهده شده در نمونه که به صورت تصادفی از جامعه انتخاب شده است، مقداری برابر با میانگین مفروض جامعه دارد یا خیر، به کار می رود.
برای مثال میانگین افسردگی دانشجویان دانشگاه با توجه به مقیاس GHQ[3] (گلدبرگ، ۱۹۷۳)، برابر ۷ محاسبه شده است. حال یکی از روان شناسان دانشگاه معتقد است دانشجویانی که ورزش می کنند افسردگی کمتری دارند. بر همین اساسس ۱۰۰ نفر از دانشجویان ورزشکار را به صورت تصادفی انتخاب کرده و میزان افسردگی آنان را اندازه گیری می کند، میانگین افسردگی این دانشجویان برابر ۶ به دست می آید. آیا این تفاوت ۱ نمره ای بین میانگین افسردگی دانشجویان ورزشکار و میانگین افسردگی جامعه دانشجویی یک تفاوت واقعی است یا اینکه بر اساس ادعای فرض صفر، حاصل خطای نمونه گیری است و تفاوت واقعی بین نمونه و جامعه وجود ندارد.
از آنجایی که این پژوهشگر انحراف استاندارد جامعه را نمی داند و می خواهد جهت بررسی معنی داری این تفاوت از یک آزمون آماری استفاده کند، آزمون t تک نمو نه ای را به کار می برد و انحراف استاندارد نمونه را به عنوان برآوردی از انحراف استاندارد جامعه در نظر می گیرد.
قبل از اینکه چگونگی محاسبه آماره آزمون تی تک نمونه ای، توضیح داده شود لازم است با تفاوت این آزمون تی با آزمون Z تک نمونه ای خانواده توزیع t، شکل توزیع های t و درجات آزادی آزمون تی استیودنت آشنا شویم.
تفاوت آزمون t با آزمون Z
آزمون آماری Z بیانگر تفاوت یک میانگین نمونه با میانگین جامعه بر حسب واحد انحراف استاندارد است. گفته شد که محاسبه Z مستلزم معلوم بودن یعنی انحراف استاندارد جامعه است زیرا برای محاسبه آن، انحراف استاندارد توزیع میانگین ها یعنی ضرورت دارد. آزمون t نیز همین عمل مقایسه میانگین نمونه با میانگین جامعه را انجام می دهد اما برای موقعیت هایی که اطلاع دقیقی از انحراف استاندارد جامعه در دست نباشد. در این آزمون به جای انحراف استاندارد جامعه از برآوردد آن یعنی انحراف استاندارد نمونه (S) استفاده می شود. درست همان گونه که میانگین نمونهبه عنوان برآورد میانگین جامعهقابل محاسبه است. می توان انحراف استاندارد نمونه را نیز برآوردی برای انحراف استاندارد جامعه دانست.
بدین ترتیب در آزمون t تک نمونه ای (S) را که برآوردی از انحراف استاندارد جامعه از روی نمونه است به جای مقدار واقعی انحراف استاندارد جامعه قرار داده و آزمون فرض را انجام می دهیم. بنابراین آزمون t تک نمونه ای برای میانگین های جامعه باا آزمون Z تک نمونه ای مشابه است. زیرا در هر دو مورد فرضیه ای را درباره میانگین جامعه می آزماییم.
از لحاظ تفسیر نتیجه به دست آمده از این دو آزمون Z و t می توان گفت که همان گونه که نسبت Z بیانگر تفاوت میانگین نمونه از میانگین جامعه یا میانگین فرضی توزیع میانگین های نمونه ها بر حسب اندازه واحد انحراف استاندارد جامعه است. آزمون تی استیودنت نیز برآوردی برای تفاوت میانگین نمونه است. برای فهم بیشتر تفاوت و تشابه بین این دو آزمون در پژوهش و آزمون فرضیه به مثال زیر توجه کنید:
مشاور یکی از دبیرستان های شهر تهران معتقد است که دانش آموزان این دبیرستان از بهره هوشی بالا و سلامت روانی خوبی برخوردار هستند لذا این مشاور که در امر پژوهش نیز تخصص دارد ۱۰ دانش آموز این دبیرستان را به طور تصادفی انتخاب کرده و با استفاده از مقیاس هوش وکسلر و مقیاس سلامت روانی (GHQ)، بهره هوشی و سلامت روانی این دانش آموزان را اندازه گیری می کند. میانگین بهره هوشی و سلامت روانی آنها به ترتیب برابر ۱۲۰ و ۲۰ به دست می آید. با توجه به اینکه میانگین بهره هوشی برای کل جامعه دانش آموزان دبیرستانی ۱۰۰ و انحراف معیار آن ۱۰ است، این پژوهشگر برای آزمون فرض تفاوت میانگین بهره هوشی بین نمونه انتخاب شده با کل جامعه از آزمون Z تک نمونه ای استفاده می کند ولی در رابطه با سلامت روانی به دلیل اینکه پژوهشگر از میانگین و انحراف استاندارد سلامت روانی جامعه دانش آموزان دبیرستانی بی اطلاع است امکان استفاده از آزمون Z تک نمونه ای برای وی میسر نیست.
او تنها می داند که نقطه برش یا میانگین مورد انتظار مقیاس سلامت روانی را که با GHQ نشان می دهند برابر ۲۸ است. لذا در اینجا آزمون تی استیودنت تک نمونه ای، آزمون مناسبی برای مقایسه سلامت روانی نمونه با میانگین مورد انتظار خواهد بود زیرا در این آزمون با برآورد انحراف استاندارد جامعه از روی انحراف استاندارد نمونه مشکل مربوط به محدود بودن اطلاعات خود از جامعه را حل می کند.
خانواده توزیع t و درجه آزادی
توزیع های t شبیه توزیع طبیعی زنگوله ای شکل و متقارن هستند اما برخلاف توزیع طبیعی از کشیدگی های مختلف برخوردار هستند. هر چقدر حجم نمونه بزرگ تر باشد از کشیدگی توزیع t کاسته می شود و در نمونه هایی با حجم بزرگ تر ( ۱۲۰< n) شکل توزیع t تقریبا با توزیع طبیعی یکسان می شود. میانگین توزیع های t همانند توزیع طبیعی Z برابر صفر است اما انحراف استاندارد آنها بیشتر از ۱ است هر چقدر حجم نمونه بیشتر شود، انحراف استاندارد توزیع t به عدد ۱ نزدیک تر می شود. انحراف استاندارد توزیع t تقریبا از رابطه زیر محاسبه می شود.
در توزیع t به علت این که انحراف استاندارد جامعه نامعلوم است، انحراف استاندارد برآورد شده نمونه (S) به کار می رود و این فرآیند برآورد از روی S منجر به تغییر کشیدگی توزیع t می شود به طوری که در آزمون Z ، توزیع نرمال استاندارد به کار می رود ولی در آزمون t، یکی از توزیع های خانواده t که تعداد آنها بر حسب حجم نمونه متعدد است استفاده می شود. حال در آزمون t بخصوص برای مقایسه میانگین نمونه با میانگین جامعه از کدامیک از توزیع های خانواده t استفاده می کنیم؟
در جواب باید گفت که در استفاده از آزمون تی به درجات آزادی توجه می کنیم. در آزمون t تک نمونه ای درجات آزادی عبارت است از حجم نمونه منهای ۱، یعنی df = n – ۱ . به عبارت دیگر اگر حجم نمونه ۱۰ نفر باشد درجه آزادی ۹ است. بنابراین از بین خانواده توزیع های t ما از توزیع استفاده خواهیم کرد که با ۹ درجه آزادی تنظیم شده است.
چنانچه اندازه نمونه افزایش پیدا کند درجه آزادی به سمت بی نهایت میل کند، شکل توزیع t به شکل Z توزیع نرمال نزدیک تر می شود و در بی نهایت هر دو توزیع t و نرمال یکی می شوند.
شکل توزیع t
شکل توزیع های t با شکل توزیع نرمال استاندارد از این لحاظ که هر دو توزیع تک نمایی و متقارن هستند شباهت دارد، اما تفاوت آنها در این است که توزیع t دارای کشیدگی بیشتری است و سطح واقع در زیر بخش های انتهایی اندکی بیشتر از توزیع نرمال استاندارد است. در شکل (۴-۱) دو توزیع t با درجات آزادی مختلف ۱۰ و ۲۵ را همراه با توزیع نرمال استاندارد نشان داده ایم.
شکل۴-۱:یک توزیع نرمال و دو توزیع t با درجه آزادی ۱۰ و ۲۵ نشان داده می شود.
| به ادامه مطلب توجه بفرمایید |
همان طوری که ملاحظه می کنید چون سطح زیر توزیع ها در دنباله ها نسبت به توزیع نرمال بیشتر است. بنابراین برای جدا ساختن ۵/۲ درصد سطح بالای توزیع Z در توزیع نرمال استاندارد نیاز به نمره t بالاتری است. مثلا در توزیع نرمال ۵/۲ درصد همه مشاهده ها بالاتر از Z = +1/96 قرار دارد در حالی که در توزیع t باdf = 10 درجه آزادی ۵/۲ درصد همه مشاهده ها بالاتر از t = +2/23 قرار می گیرد.
به عبارت دیگر برای رد فرض صفر با استفاده از t در مقایسه با Z احتیاج به نسبت t بزرگ تری است ولی هر چقدر که تعداد درجات آزادی همراه با توزیع t افزایش یابد، توزیع مذکور شباهت بیشتری به توزیع نرمال پیدا می کند. برای مثال چنانکه در شکل ۴-۱ ملاحظه کردید توزیع t با df = 25 بیش از توزیع t با df = 10 به توزیع نرمال شباهت دارد و نمره ۵/۹۷ درصدی در توزیع t با df = 25 برابر با = +۲/۰۶ است که به مقدار متناظر آن در توزیع نرمال استاندارد Z = +1/96 نزدیک است.
بنابراین همان طور که قبلا گفتیم اگر درجات آزادی همراه با توزیع t باز هم افزایش یابد توزیع مذکور به توزیع نرمال استاندارد نزدیک تر می شود و در حالت df = ، شکل دو توزیع بر هم منطبق می شوند زیرا اگر نمونه بی نهایت باشد، برآورد انحراف جامعه از روی انحراف معیار نمونه (S) کامل و بنابراین مقدار برآورده شده از انحراف معیار جامعه دقیق خواهد بود و بهه همین دلیل است که در این موقعیت آزمون t به آزمون ZZ تبدیل می شود.
چگونگی محاسبه آزمون تک نمونه ای t
برای محاسبه آزمون تک نمونه ای t همانند محاسبه سایر آزمون ها از جمله آنچه برای آزمون Z گفته شد باید مراحل زیر طی شود:
- گام اول فرضی که قرار است آزمایش شود و فرض مخالف آن بیان شود در آزمون تک نمونه ای فرض صفر بیان می کند که میانگین نمونه مساوی است با میانگین جامعه ای که نمونه از آن انتخاب شده است. فرض به این شکل نوشته می شود:
فرض خلاف مدعی وجود تفاوت بین میانگین محاسبه شده نمونه با میانگین جامعه مربوط به آن است. این فرض می تواند به صورت بدون جهت و یا جهت دار بیان شود. فرض خلاف بدون جهت ادعا می کند که میانگین نمونه با میانگین جامعه مورد نظر تفاوت دارد ولی جهت آن تفاوت را بیان نمی کند ولی در فرض خلاف جهت دار، جهت تفاوت بین میانگین نمونه و میانگین جامعه بیان می شود.
مثلا ( یعنی میانگین جامعه از میانگین نمونه بیشتر است ) یا ( یعنی میانگین جامعه از میانگین نمونه کوچک تر است ). برای فرض های بدون جهت، آزمون دو دامنه و برای فرض های جهت دار آزمون یک دامنه مورد استفاده قرار می گیرد.
برای توضیح فرض صفر و فرض خلاف در آزمون t تک نمونه ای چند مثال ذکر می کنیم که در هر یک از آنها میانگین فرضی جامعه به عنوان فرض صفر تعیین می شود. قبل از ذکر مثال ها لازم است بدانیم که میانگین فرضی جامعه معمولا بر اساس پژوهش های قبلی تعیین می شود. گاهی نیز نقطه وسط متغییر و یا میانگین مورد انتظار مقیاس مورد استفاده برای میانگین فرضی جامعه در نظر گرفته می شود.
در مثال های زیر جهت تعیین فرض صفر با استفاده از میانگین های فرضی جامعه هر دو حالت را ملاحظه خواهید کرد.
مثال ۱. نتایج پژوهش ها نشان داده است که میانگین نمره های استعداد کلامی برای جامعه داوطلب ورود به دانشگاه ۵۰۰ است، سوال مورد پرسش این است که آیا نمره دانشجویان سال اول دانشگاه به طور متوسط از جامعه دانش آموزان داوطلب ورود به دانشگاه بیشتر است؟ برای پاسخ به این سوال که آیا نمونه مورد بررسی از جامعه ای با میانگین ۵۰۰ انتخاب شده یا از جامعه ای دیگر، از آزمون t استفاده می شود. فرض صفر و فرض مقابل این گونه نوشته می شوند:
فرض مقابل یک فرض جهت دار و آزمون به کار رفته یک دامنه است.
مثال ۲. پژوهشگری می خواهد میزان سلامت روانی پرستاران شیفت شب بیمارستان ها را بررسی کند به همین منظور از مقیاس سلامت روانی GHQ ( گلدبرگ، ۱۹۷۳ ) استفاده می کند. او از ۱۶ پرستار شیفت شب بیمارست
توزیع آماره آزمون تی استیودنت
توزیع تی
در هنگام تعیین تقریبی میانگین نمونههای برداشته شده از یک متغیر تصادفی، توزیع تی-استودنت (بهانگلیسی: Student’s t-distribution) مطرح میشود. این توزیع اساس آزمونی به نام “تست تی” است که مقدار اطمینان از تفاوت دو متغیر تصادفی را از روی نمونههایشان اعلام میکند.
وجه تسمیه
فردی که برای اولین بار بر روی موضوع کار میکرد (ویلیام سیلی گوسه William Sealy Gosset)، گویا نمیتوانست به نام اصلیش مقالاتش را امضا کند و به ناچار از نام مستعار استیودنت (شاگرد) استفاده میکرد.
چگونگی ساخته شدن توزیع آزمون تی استودنت
…..
آزمون t
آزمون تی استیودنت، توزیع یا در حقیقت خانوادهای از توزیعها است که با استفاده از آنها فرضیههایی را در باره نمونه در شرایط جامعه ناشناخته است، آزمون میکنیم. اهمیت این آزمون (توزیع) در آن است که پژوهشگر را قادر میسازد با نمونههای کوچکتر (حداقل ۲ نفر) اطلاعاتی در باره جامعه بدست آورد. آزمون t شامل خانوادهای از توزیعها است (برخلاف آزمون z) و اینگونه فرض میکند، که هر نمونهای دارای توزیع مخصوص به خود است، که شکل این توزیع از طریق محاسبه درجات آزادی (Degrees of Freedom) مشخص میشود.
به عبارت دیگر توزیع t تابع درجات آزادی است و هر چه درجات آزادی (d.F) افزایش پیدا کند به توزیع طبیعی نزدیکتر میشود. هرچه درجات آزادی کاهش یابد، پراکندگی بیشتر میشود. خود درجات آزادی نیز تابعی از اندازه نمونه انتخابی هستند. هر چه تعداد نمونه بیشتر باشد بهتر است. از آزمون t میتوان برای تجزیه و تحلیل میانگین در پژوهشهای تک متغیری یک گروهی و دو گروهی و چند متغیری دو گروهی استفاده کرد.
فرض کنید که X1, …, Xn متغیرهای تصادفی مستقل نرمال با میانگین μ و واریانس σ۲ هستند.
اگر میانگین n نمونه فوق مقدار:
و واریانس آن :
باشند. میتوان به راحتی اثبات کرد که متغیر Z:
یک متغیر تصادفی نرمال با میانگین صفر و واریانس ۱ است.
حال به جای متغیر Z فوق، متغیر T را به صورت زیر تعریف میکنیم.
فرق این متغیر با Z، در این است که به جای (مقدار واقعی واریانس) از مقدار تخمینی آن . استفاده شده است. میتوان نشان داد که متغیر T تابع توزیع احتمالی به فرم زیر دارد.
که ν (که درجه آزادی تابع است) برابر است با n − ۱ و Γ تابع گاما است.
تابع فوق را به صورت زیر نیز میتوان نگاشت:
که در آن B، تابع بتا است.
همانطور که دیده میشود، تابع توزیع نسبت به μ یا σ مستقل است.
ممانهای این تابع توزیع به صورت زیر هستند.
اگر ۰ < k < ν و k زوج باشد، با توجه به خواص تابع گاما، ممانها به صورت زیر ساده میشوند:
تست تی
برای بررسی این نکته که آیا میانگین نمونههای برداشته شده از یک متغیر تصادفی تا چه حد به میزان “واقعی” (که آزمایشگر نمیداند) نزدیک است از تست تی-استیودنت استفاده میشود.
- مثال: میانگین طول عمر ۱۵ بیمار سرطانی که داروی الف را مصرف کردند ۱۱۰ روز است با واریانس ۱۵. میانگین طول عمر ۱۵ بیمار دیگر که داروی مورد آزمایش را مصرف نکردند، ۱۰۰ روز گشته است با واریانس ۱۲. سوال: آیا بهبود در میانگین طول عمر بیمارانی که از داروی جدید استفاده کردند ناشی از عملکرد دارو است یا خطای میانگینگیری ناشی از تعداد محدود نمونهها؟
- جواب:
فرض صفر این مسئله را این قرار میدهیم که دارو اثری نداشته است. یا به عبارت دیگر میشود این طور فرض کرد که نمونههای برداشته شده از هر دو گروه، در واقع نمونهگیری از یک متغیر تصادفی است. در این مسئله، ما فرض صفر خود را هنگامی نقض میکنیم، که به احتمال ۹۵ درصد مطمئن شویم که غلط است. (این عدد اختیاری است)
این یک مسئله با ۱۴ درجه آزادی و دوطرفه است. پس از جدول مقادیر توزیع t، مقداری را که از تقاطع ۰.۹۷۵ درصد (مقادیر جدول از احتمال یک طرفه حاصل شدهاند) و ۱۴ درجه آزادی حاصل میشود را میابیم: ۲.۱۴۵. این مقدار را اگر در ورایانس اختلاف نمونهها ضرب کنیم (در محاسبه این واریانس فرض مستقل بودن را نیز کردهایم) و بر ریشه ۱۵ تقسیم کنیم عدد ۱۰.۵۸ حاصل میگردد.
پس به احتمال ۹۵ درصد، اگر دارو اثری نداشته باشد، باید اختلاف میانگین دو نمونه بین مثبت و منفی ۱۰.۵۸ باشد. که در این مثال هست. پس با قطعیت نمیتوان از اثر مثبت دارو صحبت کرد.
جدول مقادیر
توجه کنید که مقادیر این جدول از احتمال یک طرفه به دست آمدهاند. برای استفاده از آن در مسائل دوطرفه باید ابتدا مقدار احتمال را به یک طرفه تبدیل کنید. مثالا در ۹۰ درصد در احتمال دوطرفه، میشود ۹۵ درصد یک طرفه.
| ν | ۷۵٪ | ۸۰٪ | ۸۵٪ | ۹۰٪ | ۹۵٪ | ۹۷٫۵٪ | ۹۹٪ | ۹۹٫۵٪ | ۹۹٫۷۵٪ | ۹۹٫۹٪ | ۹۹٫۹۵٪ |
| ۱ | ۱٫۰۰۰ | ۱٫۳۷۶ | ۱٫۹۶۳ | ۳٫۰۷۸ | ۶٫۳۱۴ | ۱۲٫۷۱ | ۳۱٫۸۲ | ۶۳٫۶۶ | ۱۲۷٫۳ | ۳۱۸٫۳ | ۶۳۶٫۶ |
| ۲ | ۰٫۸۱۶ | ۱٫۰۶۱ | ۱٫۳۸۶ | ۱٫۸۸۶ | ۲٫۹۲۰ | ۴٫۳۰۳ | ۶٫۹۶۵ | ۹٫۹۲۵ | ۱۴٫۰۹ | ۲۲٫۳۳ | ۳۱٫۶۰ |
| ۳ | ۰٫۷۶۵ | ۰٫۹۷۸ | ۱٫۲۵۰ | ۱٫۶۳۸ | ۲٫۳۵۳ | ۳٫۱۸۲ | ۴٫۵۴۱ | ۵٫۸۴۱ | ۷٫۴۵۳ | ۱۰٫۲۱ | ۱۲٫۹۲ |
| ۴ | ۰٫۷۴۱ | ۰٫۹۴۱ | ۱٫۱۹۰ | ۱٫۵۳۳ | ۲٫۱۳۲ | ۲٫۷۷۶ | ۳٫۷۴۷ | ۴٫۶۰۴ | ۵٫۵۹۸ | ۷٫۱۷۳ | ۸٫۶۱۰ |
| ۵ | ۰٫۷۲۷ | ۰٫۹۲۰ | ۱٫۱۵۶ | ۱٫۴۷۶ | ۲٫۰۱۵ | ۲٫۵۷۱ | ۳٫۳۶۵ | ۴٫۰۳۲ | ۴٫۷۷۳ | ۵٫۸۹۳ | ۶٫۸۶۹ |
| ۶ | ۰٫۷۱۸ | ۰٫۹۰۶ | ۱٫۱۳۴ | ۱٫۴۴۰ | ۱٫۹۴۳ | ۲٫۴۴۷ | ۳٫۱۴۳ | ۳٫۷۰۷ | ۴٫۳۱۷ | ۵٫۲۰۸ | ۵٫۹۵۹ |
| ۷ | ۰٫۷۱۱ | ۰٫۸۹۶ | ۱٫۱۱۹ | ۱٫۴۱۵ | ۱٫۸۹۵ | ۲٫۳۶۵ | ۲٫۹۹۸ | ۳٫۴۹۹ | ۴٫۰۲۹ | ۴٫۷۸۵ | ۵٫۴۰۸ |
| ۸ | ۰٫۷۰۶ | ۰٫۸۸۹ | ۱٫۱۰۸ | ۱٫۳۹۷ | ۱٫۸۶۰ | ۲٫۳۰۶ | ۲٫۸۹۶ | ۳٫۳۵۵ | ۳٫۸۳۳ | ۴٫۵۰۱ | ۵٫۰۴۱ |
| ۹ | ۰٫۷۰۳ | ۰٫۸۸۳ | ۱٫۱۰۰ | ۱٫۳۸۳ | ۱٫۸۳۳ | ۲٫۲۶۲ | ۲٫۸۲۱ | ۳٫۲۵۰ | ۳٫۶۹۰ | ۴٫۲۹۷ | ۴٫۷۸۱ |
| ۱۰ | ۰٫۷۰۰ | ۰٫۸۷۹ | ۱٫۰۹۳ | ۱٫۳۷۲ | ۱٫۸۱۲ | ۲٫۲۲۸ | ۲٫۷۶۴ | ۳٫۱۶۹ | ۳٫۵۸۱ | ۴٫۱۴۴ | ۴٫۵۸۷ |
| ۱۱ | ۰٫۶۹۷ | ۰٫۸۷۶ | ۱٫۰۸۸ | ۱٫۳۶۳ | ۱٫۷۹۶ | ۲٫۲۰۱ | ۲٫۷۱۸ | ۳٫۱۰۶ | ۳٫۴۹۷ | ۴٫۰۲۵ | ۴٫۴۳۷ |
| ۱۲ | ۰٫۶۹۵ | ۰٫۸۷۳ | ۱٫۰۸۳ | ۱٫۳۵۶ | ۱٫۷۸۲ | ۲٫۱۷۹ | ۲٫۶۸۱ | ۳٫۰۵۵ | ۳٫۴۲۸ | ۳٫۹۳۰ | ۴٫۳۱۸ |
| ۱۳ | ۰٫۶۹۴ | ۰٫۸۷۰ | ۱٫۰۷۹ | ۱٫۳۵۰ | ۱٫۷۷۱ | ۲٫۱۶۰ | ۲٫۶۵۰ | ۳٫۰۱۲ | ۳٫۳۷۲ | ۳٫۸۵۲ | ۴٫۲۲۱ |
| ۱۴ | ۰٫۶۹۲ | ۰٫۸۶۸ | ۱٫۰۷۶ | ۱٫۳۴۵ | ۱٫۷۶۱ | ۲٫۱۴۵ | ۲٫۶۲۴ | ۲٫۹۷۷ | ۳٫۳۲۶ | ۳٫۷۸۷ | ۴٫۱۴۰ |
| ۱۵ | ۰٫۶۹۱ | ۰٫۸۶۶ | ۱٫۰۷۴ | ۱٫۳۴۱ | ۱٫۷۵۳ | ۲٫۱۳۱ | ۲٫۶۰۲ | ۲٫۹۴۷ | ۳٫۲۸۶ | ۳٫۷۳۳ | ۴٫۰۷۳ |
| ۱۶ | ۰٫۶۹۰ | ۰٫۸۶۵ | ۱٫۰۷۱ | ۱٫۳۳۷ | ۱٫۷۴۶ | ۲٫۱۲۰ | ۲٫۵۸۳ | ۲٫۹۲۱ | ۳٫۲۵۲ | ۳٫۶۸۶ | ۴٫۰۱۵ |
| ۱۷ | ۰٫۶۸۹ | ۰٫۸۶۳ | ۱٫۰۶۹ | ۱٫۳۳۳ | ۱٫۷۴۰ | ۲٫۱۱۰ | ۲٫۵۶۷ | ۲٫۸۹۸ | ۳٫۲۲۲ | ۳٫۶۴۶ | ۳٫۹۶۵ |
| ۱۸ | ۰٫۶۸۸ | ۰٫۸۶۲ | ۱٫۰۶۷ | ۱٫۳۳۰ | ۱٫۷۳۴ | ۲٫۱۰۱ | ۲٫۵۵۲ | ۲٫۸۷۸ | ۳٫۱۹۷ | ۳٫۶۱۰ | ۳٫۹۲۲ |
| ۱۹ | ۰٫۶۸۸ | ۰٫۸۶۱ | ۱٫۰۶۶ | ۱٫۳۲۸ | ۱٫۷۲۹ | ۲٫۰۹۳ | ۲٫۵۳۹ | ۲٫۸۶۱ | ۳٫۱۷۴ | ۳٫۵۷۹ | ۳٫۸۸۳ |
| ۲۰ | ۰٫۶۸۷ | ۰٫۸۶۰ | ۱٫۰۶۴ | ۱٫۳۲۵ | ۱٫۷۲۵ | ۲٫۰۸۶ | ۲٫۵۲۸ | ۲٫۸۴۵ | ۳٫۱۵۳ | ۳٫۵۵۲ | ۳٫۸۵۰ |
| ۲۱ | ۰٫۶۸۶ | ۰٫۸۵۹ | ۱٫۰۶۳ | ۱٫۳۲۳ | ۱٫۷۲۱ | ۲٫۰۸۰ | ۲٫۵۱۸ | ۲٫۸۳۱ | ۳٫۱۳۵ | ۳٫۵۲۷ | ۳٫۸۱۹ |
| ۲۲ | ۰٫۶۸۶ | ۰٫۸۵۸ | ۱٫۰۶۱ | ۱٫۳۲۱ | ۱٫۷۱۷ | ۲٫۰۷۴ | ۲٫۵۰۸ | ۲٫۸۱۹ | ۳٫۱۱۹ | ۳٫۵۰۵ | ۳٫۷۹۲ |
| ۲۳ | ۰٫۶۸۵ | ۰٫۸۵۸ | ۱٫۰۶۰ | ۱٫۳۱۹ | ۱٫۷۱۴ | ۲٫۰۶۹ | ۲٫۵۰۰ | ۲٫۸۰۷ | ۳٫۱۰۴ | ۳٫۴۸۵ | ۳٫۷۶۷ |
| ۲۴ | ۰٫۶۸۵ | ۰٫۸۵۷ | ۱٫۰۵۹ | ۱٫۳۱۸ | ۱٫۷۱۱ | ۲٫۰۶۴ | ۲٫۴۹۲ | ۲٫۷۹۷ | ۳٫۰۹۱ | ۳٫۴۶۷ | ۳٫۷۴۵ |
| ۲۵ | ۰٫۶۸۴ | ۰٫۸۵۶ | ۱٫۰۵۸ | ۱٫۳۱۶ | ۱٫۷۰۸ | ۲٫۰۶۰ | ۲٫۴۸۵ | ۲٫۷۸۷ | ۳٫۰۷۸ | ۳٫۴۵۰ | ۳٫۷۲۵ |
| ۲۶ | ۰٫۶۸۴ | ۰٫۸۵۶ | ۱٫۰۵۸ | ۱٫۳۱۵ | ۱٫۷۰۶ | ۲٫۰۵۶ | ۲٫۴۷۹ | ۲٫۷۷۹ | ۳٫۰۶۷ | ۳٫۴۳۵ | ۳٫۷۰۷ |
| ۲۷ | ۰٫۶۸۴ | ۰٫۸۵۵ | ۱٫۰۵۷ | ۱٫۳۱۴ | ۱٫۷۰۳ | ۲٫۰۵۲ | ۲٫۴۷۳ | ۲٫۷۷۱ | ۳٫۰۵۷ | ۳٫۴۲۱ | ۳٫۶۹۰ |
| ۲۸ | ۰٫۶۸۳ | ۰٫۸۵۵ | ۱٫۰۵۶ | ۱٫۳۱۳ | ۱٫۷۰۱ | ۲٫۰۴۸ | ۲٫۴۶۷ | ۲٫۷۶۳ | ۳٫۰۴۷ | ۳٫۴۰۸ | ۳٫۶۷۴ |
| ۲۹ | ۰٫۶۸۳ | ۰٫۸۵۴ | ۱٫۰۵۵ | ۱٫۳۱۱ | ۱٫۶۹۹ | ۲٫۰۴۵ | ۲٫۴۶۲ | ۲٫۷۵۶ | ۳٫۰۳۸ | ۳٫۳۹۶ | ۳٫۶۵۹ |
| ۳۰ | ۰٫۶۸۳ | ۰٫۸۵۴ | ۱٫۰۵۵ | ۱٫۳۱۰ | ۱٫۶۹۷ | ۲٫۰۴۲ | ۲٫۴۵۷ | ۲٫۷۵۰ | ۳٫۰۳۰ | ۳٫۳۸۵ | ۳٫۶۴۶ |
| ۴۰ | ۰٫۶۸۱ | ۰٫۸۵۱ | ۱٫۰۵۰ | ۱٫۳۰۳ | ۱٫۶۸۴ | ۲٫۰۲۱ | ۲٫۴۲۳ | ۲٫۷۰۴ | ۲٫۹۷۱ | ۳٫۳۰۷ | ۳٫۵۵۱ |
| ۵۰ | ۰٫۶۷۹ | ۰٫۸۴۹ | ۱٫۰۴۷ | ۱٫۲۹۹ | ۱٫۶۷۶ | ۲٫۰۰۹ | ۲٫۴۰۳ | ۲٫۶۷۸ | ۲٫۹۳۷ | ۳٫۲۶۱ | ۳٫۴۹۶ |
| ۶۰ | ۰٫۶۷۹ | ۰٫۸۴۸ | ۱٫۰۴۵ | ۱٫۲۹۶ | ۱٫۶۷۱ | ۲٫۰۰۰ | ۲٫۳۹۰ | ۲٫۶۶۰ | ۲٫۹۱۵ | ۳٫۲۳۲ | ۳٫۴۶۰ |
| ۸۰ | ۰٫۶۷۸ | ۰٫۸۴۶ | ۱٫۰۴۳ | ۱٫۲۹۲ | ۱٫۶۶۴ | ۱٫۹۹۰ | ۲٫۳۷۴ | ۲٫۶۳۹ | ۲٫۸۸۷ | ۳٫۱۹۵ | ۳٫۴۱۶ |
| ۱۰۰ | ۰٫۶۷۷ | ۰٫۸۴۵ | ۱٫۰۴۲ | ۱٫۲۹۰ | ۱٫۶۶۰ | ۱٫۹۸۴ | ۲٫۳۶۴ | ۲٫۶۲۶ | ۲٫۸۷۱ | ۳٫۱۷۴ | ۳٫۳۹۰ |
| ۱۲۰ | ۰٫۶۷۷ | ۰٫۸۴۵ | ۱٫۰۴۱ | ۱٫۲۸۹ | ۱٫۶۵۸ | ۱٫۹۸۰ | ۲٫۳۵۸ | ۲٫۶۱۷ | ۲٫۸۶۰ | ۳٫۱۶۰ | ۳٫۳۷۳ |
| ۰٫۶۷۴ | ۰٫۸۴۲ | ۱٫۰۳۶ | ۱٫۲۸۲ | ۱٫۶۴۵ | ۱٫۹۶۰ | ۲٫۳۲۶ | ۲٫۵۷۶ | ۲٫۸۰۷ | ۳٫۰۹۰ | ۳٫۲۹۱ |
توزیع های مرتبط
- X˜t(ν) دارای توزیع تی است، اگر دارای توزیع عکس کایدو مقیاس شده بوده و دارای توزیع نرمال باشد.
- Y˜F(ν۱ = ۱,ν۲ = ν) دارای توزیع اف است اگر و دارای توزیع تی-استودنت باشد.
- دارای توزیع نرمال است اگر و X˜t(ν).
- X˜Cauchy(0,1) دارای توزیع کوشی است اگر X˜t(ν = ۱).
| پارامترها | ν > 0 درجات آزادی (حقیقی) |
| گستره | |
| تابع چگالی احتمال | |
| تابع توزیع تجمعی(سیدیاف) | : تابع فوقهندسی |
| میانگین | تعریف نشده برای بقیه مقادیر |
| میانه | ۰ |
| مُد | ۰ |
| واریانس | تعریف نشده برای بقیه مقادیر |
| چولگی | |
| کشیدگی | |
| انتروپی |
|
| تابع مولد گشتاور (ام جی اف) | تعریف نشده |